Resposta: UERJ 2024
Para resolver o problema, seguimos os passos detalhados abaixo:
Passo 1: O comprimento do arco descrito pela geratriz é calculado utilizando a fórmula:
Onde:
- \( \theta = 120^\circ \) (ângulo central do setor)
- \( r = 12 \, \text{cm} \) (raio do setor, que é a geratriz do cone)
Substituindo os valores:
Portanto, o comprimento do arco \( AVP \) é:
Passo 2: Como o pião rola sem deslizar, a circunferência da base do cone é igual ao comprimento do arco \( AVP \):
A fórmula da circunferência é:
Dividindo ambos os lados por \( 2\pi \), obtemos:
Passo 3: O diâmetro da base \( AB \) é o dobro do raio:
Questão 1
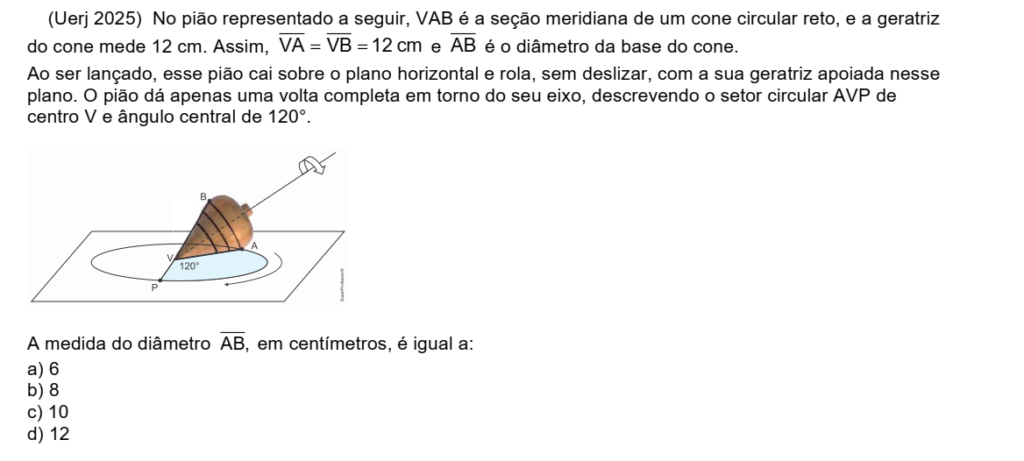
Um pião é representado por um cone circular reto cuja seção meridiana é um triângulo isósceles \( VAB \), onde \( VA = VB = 10 \, \text{cm} \), e \( AB \) é o diâmetro da base do cone. Quando o pião é lançado, ele cai sobre um plano horizontal e rola, sem deslizar, com a sua geratriz apoiada nesse plano. Ao dar uma volta completa em torno de seu eixo, o pião descreve o setor circular \( AVP \), com centro em \( V \) e ângulo central de \( 90^\circ \).
A medida do diâmetro \( AB \), em centímetros, é igual a:
- a) 5
- b) 10
- c) 15
- d) 20
- e) 25
Questão 2
Um brinquedo em forma de pião é modelado por um cone circular reto com geratriz \( g = 15 \, \text{cm} \), onde \( VA = VB = 15 \, \text{cm} \), e \( AB \) é o diâmetro da base do cone. O pião, ao ser lançado, rola sem deslizar sobre um plano horizontal, com a geratriz em contato com o plano. Nesse movimento, ele descreve o setor circular \( AVP \), com centro \( V \) e ângulo central de \( 150^\circ \).
A medida do diâmetro \( AB \), em centímetros, é igual a:
- a) 10
- b) 15
- c) 20
- d) 25
- e) 30

Resolução UFPR 2023
O problema envolve determinar o tempo \( t \) para o qual o líquido em um reservatório cônico atinge metade da sua capacidade total. Abaixo está a resolução detalhada:
Passo 1: Fórmula do volume de um cone
O volume \( V \) de um cone é dado pela fórmula:
Sabemos que a área do topo (base do cone) é \( 12 \, \text{m}^2 \), e a altura do cone é \( h \). Assim, o volume total do reservatório é:
Passo 2: Metade da capacidade
O volume que corresponde à metade da capacidade total do reservatório é:
Passo 3: Volume dado pela função \( V(t) \)
O volume \( V(t) \), em função do tempo \( t \), é dado por:
Queremos saber o tempo \( t \) para o qual \( V(t) = 2h \). Substituímos na equação:
Passo 4: Resolver a equação logarítmica
Usamos a definição de logaritmo para reescrever a equação:
Isolamos \( t^2 \):
Por fim, tiramos a raiz quadrada:
Passo 5: Alternativa correta
Comparando com as alternativas, a correta é:
Questões de Matemática
Questão 1
Na figura ao lado, tem-se um reservatório no formato de um cone circular reto com altura \( h \) e área do topo igual a \( 16 \, \text{m}^2 \). Esse reservatório está sendo preenchido com um líquido cujo volume, em \( \text{m}^3 \), é dado por:
Em quanto tempo o líquido atingirá metade da capacidade desse reservatório?
a) \( t = \sqrt{3^h – 2} \)
b) \( t = \sqrt{3^{2h} – 2} \)
c) \( t = \sqrt{3^{2h} – 1} \)
d) \( t = \sqrt{3^{h} – 1} \)
e) \( t = \sqrt{4^h – 1} \)
Questão 2
Na figura ao lado, tem-se um reservatório no formato de um cone circular reto com altura \( h \) e área do topo igual a \( 10 \, \text{m}^2 \). Esse reservatório está sendo preenchido com um líquido cujo volume, em \( \text{m}^3 \), é dado por:
Em quanto tempo o líquido atingirá metade da capacidade desse reservatório?
a) \( t = \sqrt{5^{2h} – 1} \)
b) \( t = \sqrt{5^h – 3} \)
c) \( t = \sqrt{5^{h} – 2} \)
d) \( t = \sqrt{5^{h} – 3} \)
e) \( t = \sqrt{5^{2h} – 3} \)

ENEM 2023 – Resolução Interativa
Um artista plástico esculpe uma escultura a partir de um bloco de madeira de lei, em etapas. Inicialmente, esculpe um cone reto com 36 cm de altura e diâmetro da base medindo 18 cm. Em seguida, remove desse cone um cone menor, cujo diâmetro da base mede 6 cm, obtendo, assim, um tronco de cone, conforme ilustrado na figura:

Em seguida, perfura esse tronco de cone, removendo um cilindro reto, de diâmetro 6 cm, cujo eixo de simetria é o mesmo do cone original. Dessa forma, ao final, a escultura tem a forma de um tronco de cone com uma perfuração cilíndrica de base a base.
O tipo de madeira utilizada para produzir essa escultura tem massa igual a 0,6 g por centímetro cúbico de volume. Utilize 3 como aproximação para \( \pi \).
Qual é a massa, em gramas, dessa escultura?
Resolução
O volume do cone maior é dado por: \[ V_{\text{cone maior}} = \frac{1}{3} \pi R^2 h \] Substituindo os valores: \[ V_{\text{cone maior}} = \frac{1}{3} \cdot 3 \cdot 9^2 \cdot 36 = 972 \, \text{cm}^3 \]
O volume do cone menor é dado por: \[ V_{\text{cone menor}} = \frac{1}{3} \pi r^2 h_m \] Substituindo: \[ V_{\text{cone menor}} = \frac{1}{3} \cdot 3 \cdot 3^2 \cdot 12 = 108 \, \text{cm}^3 \]
O volume do tronco do cone é: \[ V_{\text{tronco}} = V_{\text{cone maior}} – V_{\text{cone menor}} = 864 \, \text{cm}^3 \]
O volume do cilindro perfurado é: \[ V_{\text{cilindro}} = \pi r^2 h = 3 \cdot 3^2 \cdot 24 = 648 \, \text{cm}^3 \]
O volume final é: \[ V_{\text{final}} = V_{\text{tronco}} – V_{\text{cilindro}} = 216 \, \text{cm}^3 \]
A massa é calculada por: \[ \text{Massa} = V_{\text{final}} \cdot \text{densidade} = 216 \cdot 0,6 = 1296,0 \, \text{g} \]
Questões de Esculturas
Questão 1
Um escultor cria uma obra a partir de um bloco de madeira. Inicialmente, ele esculpe um cone reto com altura de 45 cm e diâmetro da base de 20 cm. Em seguida, remove desse cone um cone menor com diâmetro da base de 8 cm, resultando em um tronco de cone. Depois, ele perfura esse tronco de cone com um cilindro reto cujo diâmetro é de 8 cm, de base a base.
O tipo de madeira usada tem densidade de 0,7 g/cm³. Use \( \pi = 3 \).
Qual é a massa, em gramas, dessa escultura?
Questão 2
Um artista plástico utiliza madeira de densidade 0,5 g/cm³ para criar uma escultura. Ele começa com um cone reto com altura de 50 cm e diâmetro da base de 24 cm. Em seguida, ele retira um cone menor com diâmetro da base de 10 cm e, finalmente, perfura o tronco do cone resultante com um cilindro reto de diâmetro 10 cm, de base a base.
Use \( \pi = 3 \).
Qual é a massa, em gramas, dessa escultura?
Resolução da Questão – ENEM 2022
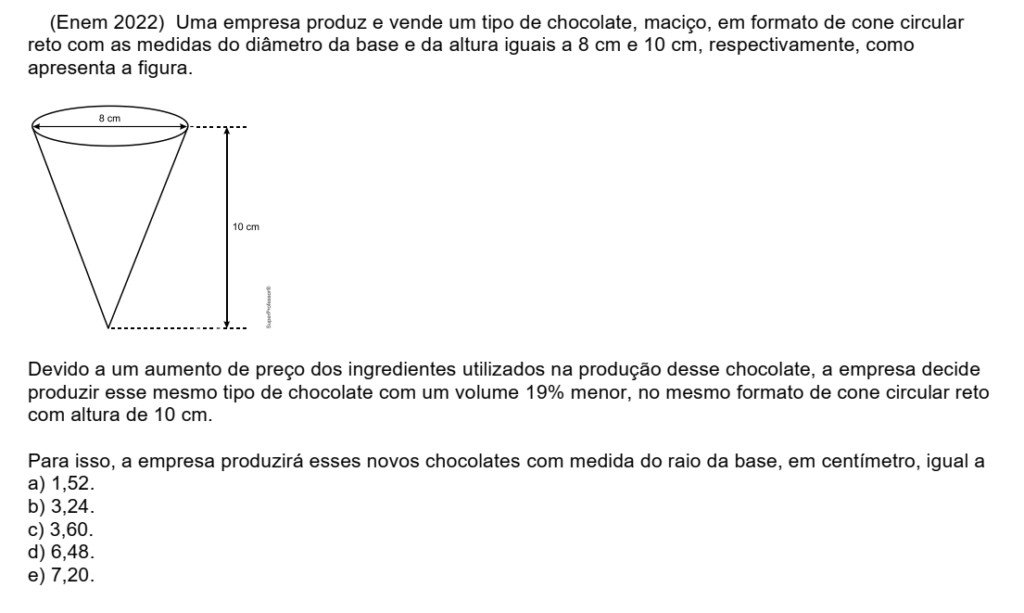
Questão: Uma empresa produz e vende um tipo de chocolate, maciço, em formato de cone circular reto com as medidas do diâmetro da base e da altura iguais a 8 cm e 10 cm, respectivamente, como apresenta a figura.
Informações: O cone original possui o diâmetro da base = 8 cm e a altura = 10 cm.
Pergunta: A empresa decide produzir esse mesmo tipo de chocolate com um volume 19% menor, no mesmo formato de cone circular reto com altura de 10 cm. Para isso, qual será a medida do raio da base no novo chocolate?
Resolução:
Passo 1: Fórmula do volume do cone:
V = (1/3) * π * r² * h
Passo 2: Cálculo do volume do cone original:
O raio da base do cone original é metade do diâmetro:
r₁ = 8 / 2 = 4 cm
Cálculo do volume do cone original (V₁):
V₁ = (1/3) * π * 4² * 10 = 160 cm³
Passo 3: O volume do novo chocolate será 19% menor que o original. Logo, o volume será:
V₂ = 160 * (1 – 0,19) = 160 * 0,81 = 129,6 cm³
Passo 4: Agora, com a altura mantida em 10 cm, vamos calcular o novo raio (r₂) utilizando a fórmula do volume do cone:
V₂ = (1/3) * π * r₂² * 10
Substituindo V₂ = 129,6 cm³:
129,6 = (1/3) * π * r₂² * 10
Agora, resolvemos para r₂²:
r₂² = 129,6 / 10 = 12,96
Passo 5: Tirando a raiz quadrada de ambos os lados:
r₂ = √12,96 ≈ 3,6 cm
Resposta: O novo raio da base do cone será aproximadamente 3,6 cm.
Alternativas:
- a) 1,52
- b) 3,24
- c) 3,60
- d) 6,48
- e) 7,20
Questões Matemáticas – ENEM
1) Uma empresa fabrica chocolates no formato de cone circular reto. O cone possui um diâmetro de 10 cm e altura de 12 cm, como apresentado na figura a seguir:
Diâmetro da base do cone = 10 cm, Altura do cone = 12 cm
Devido a um aumento no custo de produção, a empresa decide fabricar chocolates com um volume 15% menor, mantendo a altura de 12 cm. Qual será o novo valor do raio da base, em centímetros, do cone?
2) Uma fábrica de chocolates produz um cone circular reto com o diâmetro da base de 14 cm e altura de 18 cm, conforme a figura abaixo:
Diâmetro da base do cone = 14 cm, Altura do cone = 18 cm
Por conta de uma revisão nos custos de produção, a empresa decide fabricar chocolates com um volume 10% menor, mantendo a altura de 18 cm. Qual será a medida do raio da base no novo chocolate?